799. Покупка
билетов
За
билетами на премьеру нового мюзикла выстроилась очередь из n человек, каждый из
которых хочет купить один билет. На всю очередь работала только одна касса,
поэтому продажа билетов шла очень медленно, приводя "постояльцев"
очереди в отчаяние. Самые сообразительные быстро заметили, что, как правило,
несколько билетов в одни руки кассир продает быстрее, чем когда эти же билеты
продаются по одному. Поэтому они предложили нескольким стоящим подряд людям
отдавать деньги первому из них, чтобы он купил билеты на всех.
Однако
для борьбы со спекулянтами кассир продавал не более трех билетов в одни руки,
поэтому договориться таким образом между собой могли лишь два или три подряд
стоящих человека.
Известно,
что на продажу i-му человеку из очереди
одного билета кассир тратит ai
секунд, на продажу двух билетов bi секунд, трёх билетов ci секунд. Напишите
программу, которая подсчитает минимальное время, за которое можно обслужить
всех покупателей.
Обратите
внимание, что билеты на группу объединившихся людей всегда покупает первый их
них. Также никто в целях ускорения не покупает лишних билетов (то есть билетов,
которые никому не нужны).
Вход. Первое число содержит количество
покупателей в очереди n (1 ≤ n ≤ 5000). Далее идет n троек натуральных чисел ai, bi, ci.
Каждое из этих чисел не превышает 3600. Люди в очереди нумеруются начиная от
кассы.
Выход. Вывести минимальное время в
секундах, за которое можно обслужить всех покупателей.
|
Пример входа |
Пример выхода |
|
5 5 10 15 2 10 15 5 5 5 20 20 1 20 1 1 |
12 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Обозначим через t[i] минимальное время, за которое можно
обслужить покупателей с первого до i-го.
Положим t[0] = 0. Если имеется один покупатель, то он может купить себе билет
за a1 секунд, поэтому t[1]
= a1. Два покупателя либо
купят билеты каждый сам себе за a1
+ a2 секунд, либо
скооперируются и первый возьмет два билета за b1 секунд. Таким образом t[2] = min(a1 + a2, b1). При наличии трех и
более покупателей все описанные в условии задачи виды коопераций возможны,
поэтому запишем рекуррентное соотношение:
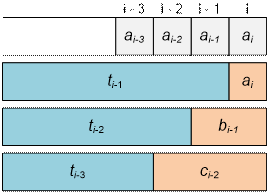
t[i]
= min(t[i – 1] + ai, t[i – 2] + bi-1, t[i
– 3] + ci-2)
Если i-ый покупатель берет билет сам, то как минимум тратится время t[i – 1] + ai.
Если (i – 1)-ый покупатель берет два билета (на себя и на i-го), то как минимум тратится время t[i – 2] + bi-1.
Если (i – 2)-ый покупатель берет три билета (на себя, на (i – 1)-го и на i-го), то как минимум тратится время t[i – 3] + ci-2.
Остается найти минимум среди трех
выражений, который равен наименьшему времени, за которое все i покупателей смогут приобрести билеты.
Реализация алгоритма
Значения ai, bi,
ci будем хранить в
массивах a, b, c.
#define MAX 5010
int a[MAX],
b[MAX], c[MAX], t[MAX];
Считываем входные данные.
scanf("%d",&n);
for(i = 1; i <= n; i++) scanf("%d %d %d",&a[i],&b[i],&c[i]);
Установим
значения ячеек .
t[0] = 0; t[1] = a[1]; t[2] = min(a[1] + a[2],b[1]);
В цикле
вычисляем значения ячеек t[i].
for(i = 3; i <= n; i++)
t[i] = min(t[i-1] +
a[i], t[i-2] + b[i-1], t[i-3] + c[i-2]);
Выводим
результат. Минимальное время, за которое можно обслужить покупателей с первого
до n-го, равно t[n].
printf("%d\n",t[n]);
Java
реализация
import
java.util.*;
public class Main
{
public static int MAX = 5010;
static int a[] = new int[MAX];
static int b[] = new int[MAX];
static int c[] = new int[MAX];
static int t[] = new int[MAX];
public static int min(int a, int b, int c)
{
return Math.min(Math.min(a,b),c);
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
for(int i = 1; i <= n; i++)
{
a[i] = con.nextInt();
b[i] = con.nextInt();
c[i] = con.nextInt();
}
t[0] = 0; t[1] = a[1]; t[2] = Math.min(a[1] + a[2],b[1]);
for(int i = 3; i <= n; i++)
t[i] = min(t[i-1] + a[i], t[i-2] + b[i-1], t[i-3] + c[i-2]);
System.out.println(t[n]);
con.close();
}
}
n = int(input())
a = [0] * 5001
b = [0] * 5001
c = [0] * 5001
for i in range(1,n+1):
a[i], b[i], c[i] = map(int, input().split())
t = [0] * (n+1)
t[0] = 0;
t[1] = a[1];
if n > 1 : t[2] = min(a[1] + a[2], b[1]);
for i in range(3, n+1):
t[i] = min(t[i-1] + a[i], t[i-2] + b[i-1], t[i-3] + c[i-2])
print(t[-1])